2024青少年编程挑战精英赛入门组题解

T1.三角形判断(triangle)

#include <bits/stdc++.h>
using namespace std;

int main() {
	freopen("triangle.in", "r", stdin);
	// 重定向标准输入流，从文件 "triangle.in" 读取输入
	freopen("triangle.out", "w", stdout);
	// 重定向标准输出流，输出结果写入文件 "triangle.out"
	int a, b, c;
	// 定义三个整数变量 a、b、c，用于存储三角形的三条边
	cin >> a >> b >> c;
	if (a + b > c && a + c > b && b + c > a) {
		// 判断三条边能否构成一个三角形，如果任意两边之和大于第三边则可以构成三角形
		if ((a == b || b == c) && a != c)
			cout << "IT";
		// 如果两条边相等且第三条边与它们不相等，输出 "IT"，表示等腰三角形
		else if (a == b && a == c && b == c)
			cout << "ET";
		// 如果三条边都相等，输出 "ET"，表示等边三角形
		else if (a * a + b * b > c * c)
			cout << "AT";
		// 如果两条边的平方和大于第三条边的平方，输出 "AT"，表示锐角三角形
		else if (a * a + b * b == c * c)
			cout << "RT";
		// 如果两条边的平方和等于第三条边的平方，输出 "RT"，表示直角三角形
		else if (a * a + b * b < c * c)
			cout << "OT";
		// 如果两条边的平方和小于第三条边的平方，输出 "OT"，表示钝角三角形
	} else
		cout << "NO";
	// 如果不能构成三角形，输出 "NO"
	return 0;
}

T2.珠算(abacus)

#include <iostream>
using namespace std;

int c[] = { 0, 1, 2, 3, 4, 1, 2, 3, 4, 5 };

int main() {
	freopen("abacus.in", "r", stdin);
	freopen("abacus.out", "w", stdout);
	int n;
	cin >> n;
	for (int i = 0; i < n; i++) {
		long long  num;
		int ans = 0;
		cin >> num;
		while (num) {
			int k = num % 10;
			ans += c[k];
			num = num / 10;
		}
		cout << ans << endl;
	}
	return 0;
}

T3.坚果保龄球(bow)

#include <iostream>
using namespace std;
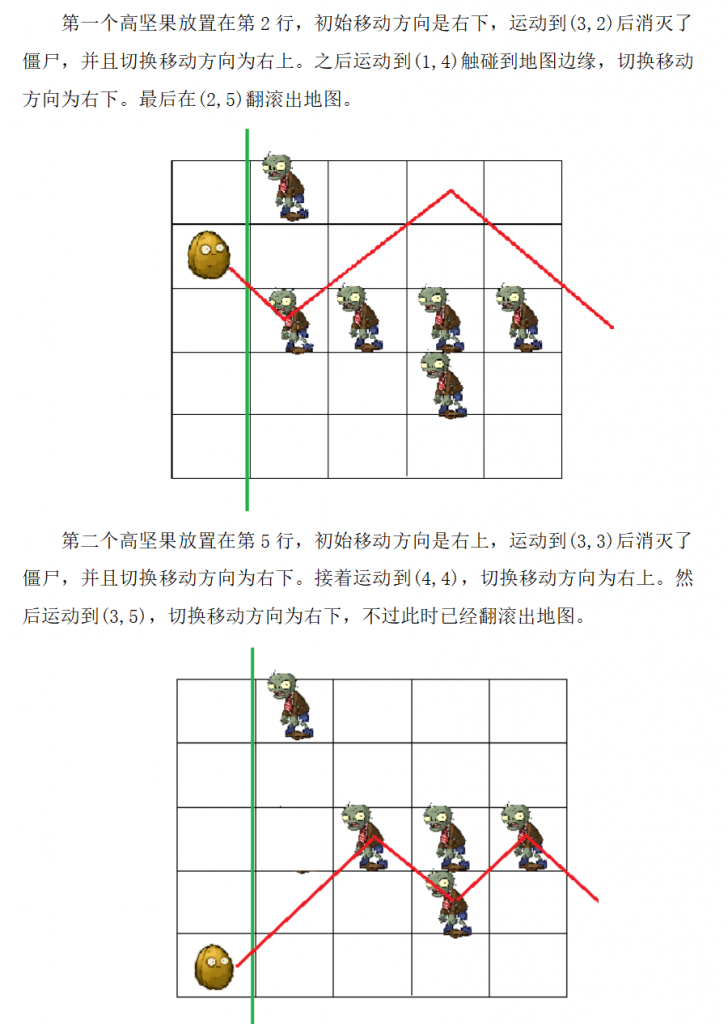
bool map[3000][3000]; // 定义二维布尔数组，用于表示地图上是否有僵尸

int main() {
	freopen("bow.in", "r", stdin); // 重定向标准输入，从文件 bow.in 读取数据
	freopen("bow.out", "w", stdout); // 重定向标准输出，输出结果到文件 bow.out

	int a, n, m;
	cin >> a >> n >> m; // 读取地图大小 a、僵尸数量 n 和高坚果数量 m
	for (int i = 0; i < n; i++) {
		int x, y;
		cin >> x >> y;
		map[x][y] = true; // 标记僵尸的位置为 true，表示该位置有僵尸
	}

	for (int i = 0; i < m; i++) {
		int x;
		int p;
		cin >> x >> p;
		if (p == 0)
			p = -1; // 如果输入的移动方向为 0，则设置为 -1，表示初始向右下移动
		for (int j = 1; j <= a; j++) {
			if (map[x][j]) {
				map[x][j] = false; // 如果当前位置有僵尸，则将其标记为已消灭
				p = -p; // 改变高坚果的移动方向
			}
			if (x == 1)
				p = 1; // 如果高坚果在最上一行，则强制向右下移动
			if (x == a)
				p = -1; // 如果高坚果在最下一行，则强制向右上移动
			x += p; // 根据移动方向更新高坚果的位置
		}
	}

	int ans = 0;
	for (int i = 1; i <= a; i++) {
		for (int j = 1; j <= a; j++) {
			if (map[i][j])
				ans++; // 统计地图上剩余僵尸的数量
		}
	}

	cout << ans; // 输出剩余僵尸的数量

	return 0;
}

T4.二叉搜索树(tree)

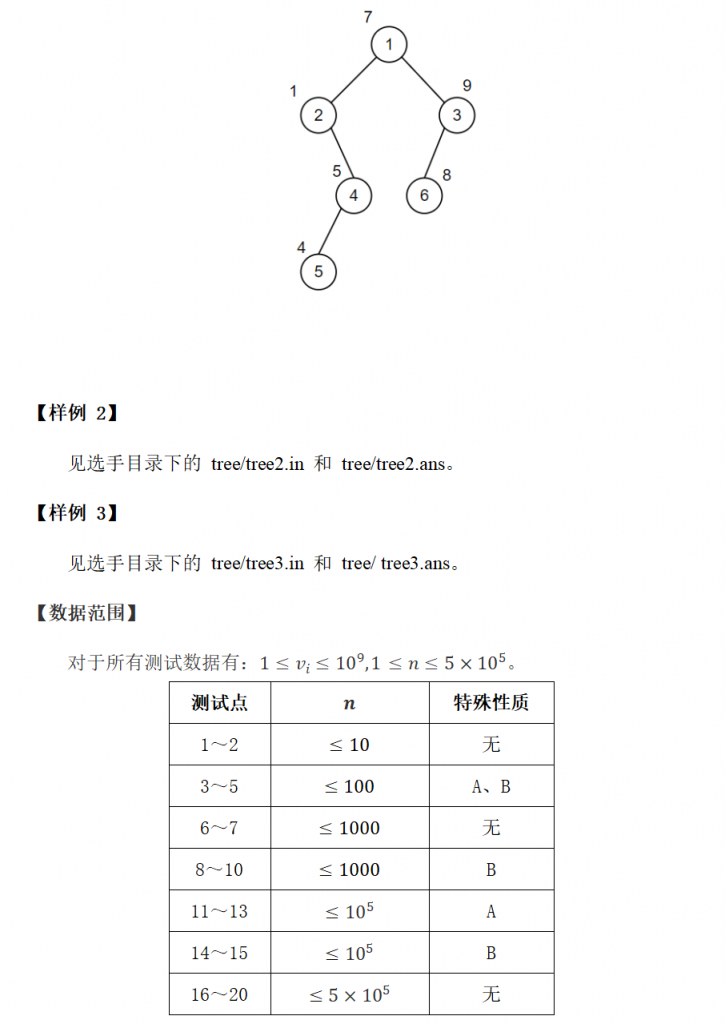
#include <iostream>
#include <algorithm>
using namespace std;
const int nsize = 500001;
// val 数组用于存储排序后的节点权值副本
int val[nsize];
// old 数组用于存储原始的节点权值
int old[nsize];
// son 二维数组用于存储每个节点的左右子节点编号
int son[nsize][2];
// siz 数组用于存储以每个节点为根的子树的大小
int siz[nsize];
// ans 用于统计不需要交换权值的节点数量
int ans = 0;

// 深度优先搜索函数 1，计算子树大小
void dfs1(int node) {
	// 如果当前节点有左子节点
	if (son[node][0])
		// 递归处理左子节点
		dfs1(son[node][0]);
	// 如果当前节点有右子节点
	if (son[node][1])
		// 递归处理右子节点
		dfs1(son[node][1]);
	// 计算以当前节点为根的子树大小
	siz[node] = 1 + siz[son[node][0]] + siz[son[node][1]];
}

// 深度优先搜索函数 2，判断节点是否在正确位置
void dfs2(int node, int left, int right) {
	// 计算在以当前节点为根的有序序列中，当前节点应该在的位置索引
	int after = left + siz[son[node][0]];
	// 如果当前节点的原始权值等于排序后在正确位置的权值
	if (old[node] == val[after])
		// 增加不需要交换权值的节点数量
		ans++;
	// 如果当前节点有左子节点
	if (son[node][0])
		// 递归处理左子节点，传入左子树的范围
		dfs2(son[node][0], left, after - 1);
	// 如果当前节点有右子节点
	if (son[node][1])
		// 递归处理右子节点，传入右子树的范围
		dfs2(son[node][1], after + 1, right);
}

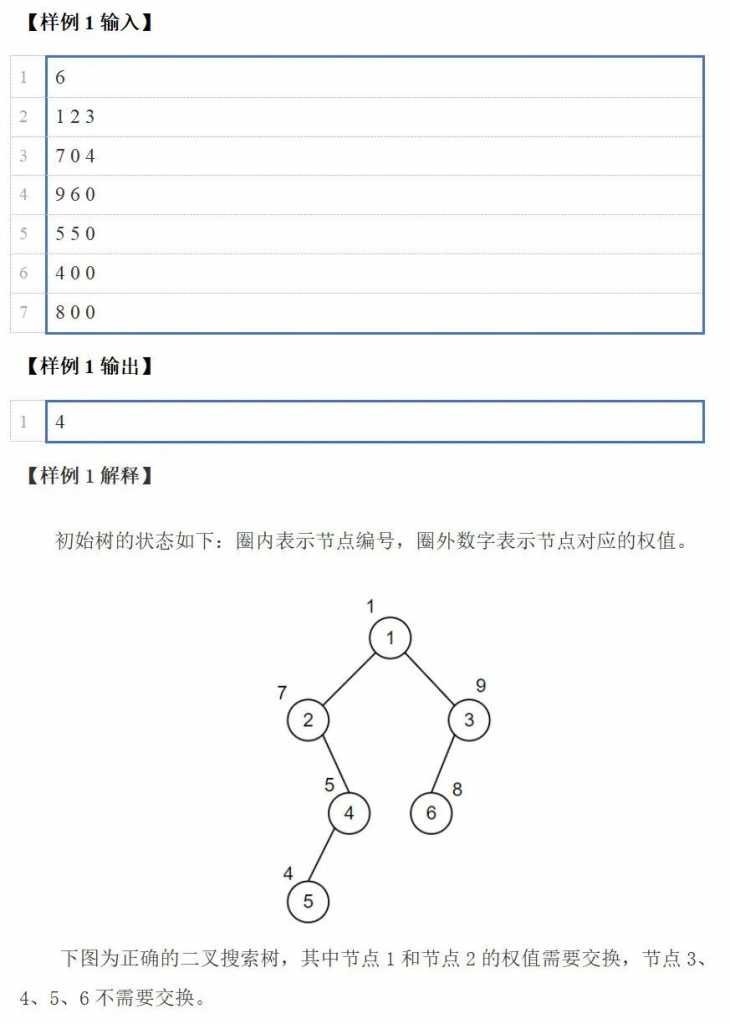
int main() {
	freopen("tree.in", "r", stdin);
	freopen("tree.out", "w", stdout);
	int n;
	cin >> n;
	// 读取每个节点的权值、左右子节点编号
	for (int i = 1; i <= n; i++) {
		cin >> old[i] >> son[i][0] >> son[i][1];
		// 将原始权值复制到 val 数组中
		val[i] = old[i];
	}
	// 对 val 数组进行排序，得到节点权值的有序序列
	sort(val + 1, val + 1 + n);
	// 从根节点开始计算子树大小
	dfs1(1);
	// 从根节点开始判断每个节点是否在正确位置
	dfs2(1, 1, n);
	// 输出不需要交换权值的节点数量
	cout << ans;
	return 0;
}

T5.强化(power)

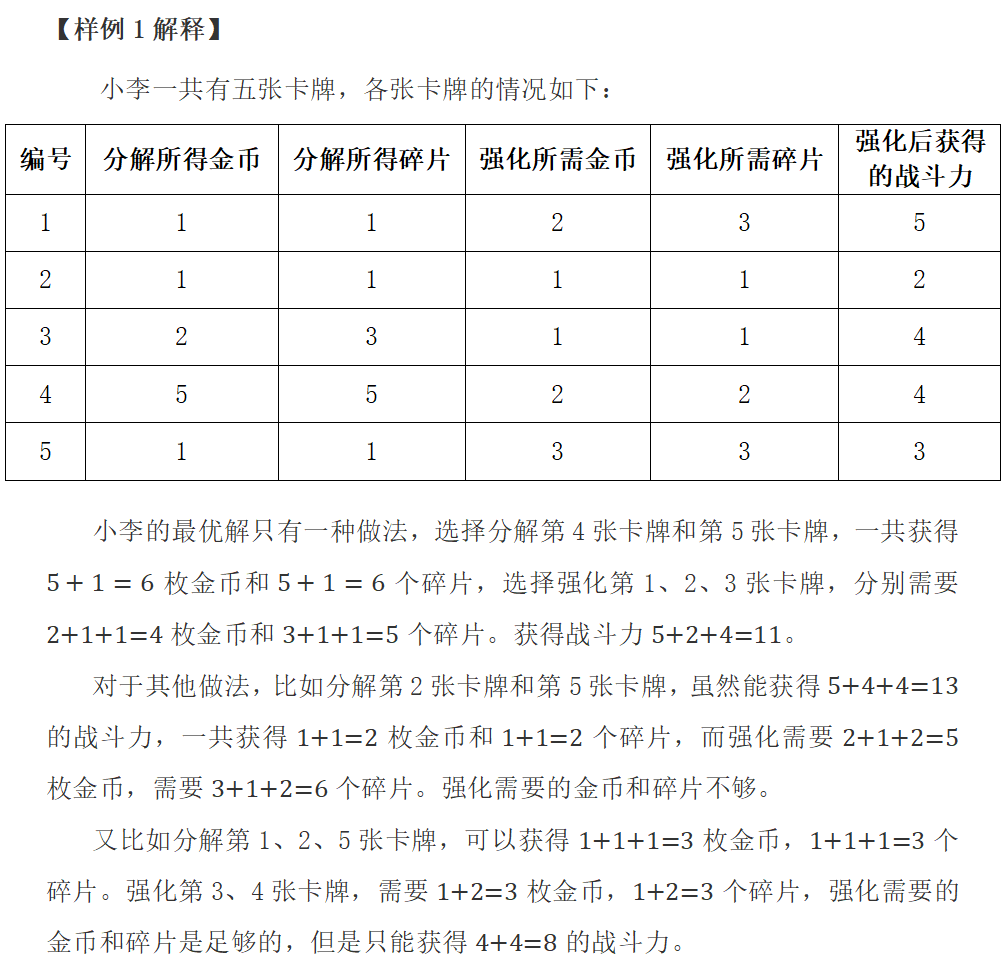
#include <iostream>
#include <cstring>
#include <fstream>
using namespace std;
const int maxValue = 1000;
// dp 数组用于存储动态规划过程中的状态值
// 第一维用于交替存储当前和上一轮的状态，第二维和第三维分别表示金币数量和碎片数量
int dp[2][maxValue * 2 + 2][maxValue * 2 + 2];

// 定义 card 结构体，用于存储每张卡牌的信息
struct card {
	int m1, s1, m2, s2, p;
};
card c[200];

int main() {
	freopen("power.in", "r", stdin);
	freopen("power.out", "w", stdout);
	int n;
	cin >> n;
	// 将 dp 数组初始化为负无穷大
	memset(dp, 0xf0, sizeof dp);
	int tfm = 0, tfs = 0, tqm = 0, tqs = 0;
	for (int i = 1; i <= n; i++) {
		cin >> c[i].m1 >> c[i].s1 >> c[i].m2 >> c[i].s2 >> c[i].p;
		// 累计所有卡牌分解获得的金币总数
		tfm += c[i].m1;
		// 累计所有卡牌分解获得的碎片总数
		tfs += c[i].s1;
		// 累计所有卡牌强化需要的金币总数
		tqm += c[i].m2;
		// 累计所有卡牌强化需要的碎片总数
		tqs += c[i].s2;
	}
	// 将状态为拥有所有卡牌强化所需的金币和碎片时的战斗力初始化为 0
	dp[0][tqm][tqs] = 0;
	for (int i = 1; i <= n; i++) {
		for (int a = 0; a < tfm + tqm; a++) {
			for (int b = 0; b < tqs + tfs; b++) {
				// 初始化当前状态为负无穷大
				dp[i & 1][a][b] = -1e9;
				// 如果当前金币和碎片数量减去卡牌 i 分解所需的金币和碎片数量后非负
				if (a - c[i].m1 >= 0 && b - c[i].s1 >= 0)
					// 更新当前状态为上一轮相应状态加上分解卡牌 i 获得的金币数（取较大值）
					dp[i & 1][a][b] = max(dp[i & 1][a][b], dp[i & 1 ^ 1][a - c[i].m1][b - c[i].s1]);
				// 如果当前金币和碎片数量加上卡牌 i 强化所需的金币和碎片数量在范围内
				if (a + c[i].m2 < maxValue * 2 && b + c[i].s2 < maxValue * 2)
					// 更新当前状态为上一轮相应状态加上强化卡牌 i 获得的战斗力（取较大值）
					dp[i & 1][a][b] = max(dp[i & 1][a][b], dp[i & 1 ^ 1][a + c[i].m2][b + c[i].s2] + c[i].p);
			}
		}
	}
	int ans = 0;
	for (int a = tqm; a <= tfm + tqm; a++) {
		for (int b = tqs; b <= tqs + tfs; b++) {
			// 找到在满足至少拥有所有卡牌强化所需的金币和碎片数量的情况下，最大的战斗力值
			ans = max(ans, dp[n & 1][a][b]);
		}
	}
	cout << ans;
	return 0;
}