第四届（2025）青少年编程挑战赛C++提高组题解

#include <iostream>
using namespace std;
int puz[1001][1001];
bool star[1001][1001];
int n;
bool ver[1001];
bool area[1001];

bool check(int i, int j) { //检查和已有星星是否有冲突
	if (ver[j])
		return false;
	if (area[puz[i][j]])
		return false;
	if (star[i - 1][j - 1] || star[i - 1][j + 1] || star[i + 1][j - 1] || star[i + 1][j + 1])
		return false;
	return true;
}
bool findAns;

void dfs(int i) { //考虑放第i行的星星
	if (i == n + 1) { //如果放完了第i行的星星即找到了答案
		findAns = true;
	} else
		for (int j = 1; j <= n; j++) {
			if (check(i, j)) {
				ver[j] = true; //标记信息
				star[i][j] = true;
				area[puz[i][j]] = true;
				dfs(i + 1);
				if (findAns)
					break; //如果找到答案，则强制退出搜索
				ver[j] = false; //擦除信息
				star[i][j] = false;
				area[puz[i][j]] = false;
			}
		}
}

int main() {
	cin >> n  ;
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			cin >> puz[i][j];
		}
	}
	dfs(1);
	if (!findAns) {
		cout << -1;
		return 0;
	}
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++)
			if (star[i][j])
				cout << i << " " << j << endl;
	}
    return 0;
}

#include "bits/stdc++.h"

using namespace std;
int cnt[500];
int n[500];
string ans;
int main() {
	int l, r;
	string s;
	cin >> l >> r >> s;
	for (char c : s) {
		cnt[c]++;
	}
	for (char c : s) {
		while (!ans.empty() && n[c] < r && ans.back() > c && n[ans.back()] + cnt[ans.back()] > l) {
			//答案字符不为空 ， 当前要插入答案的这个字符出现次数小于最大次数，答案字符最后一个字符字典序比当前要插入的这个字符还大，
			//当删掉答案的最后一个字符后，要保证这个字符在之前放到答案里面的次数，加上没有放到答案里面的次数要比 l 大，否则删了的话，出现次数不够
			//满足了上面的四个条件后，删掉答案里的最后一个字符
			n[ans.back()]--;
			ans.pop_back();
		}
		if (n[c] < r) { //如果当前的这个字符出现次数还没有超限制的话，加到答案里。
			n[c]++;
			ans.push_back(c);
		}
		cnt[c]--;
	}
	while (!ans.empty() && n[ans.back()] > l) { // 最后如果是一串连续的超过l个的相同字符，只需要保留l个就行了。
		ans.pop_back();
		n[ans.back()]--;
	}
	cout << ans;
	return 0;
}

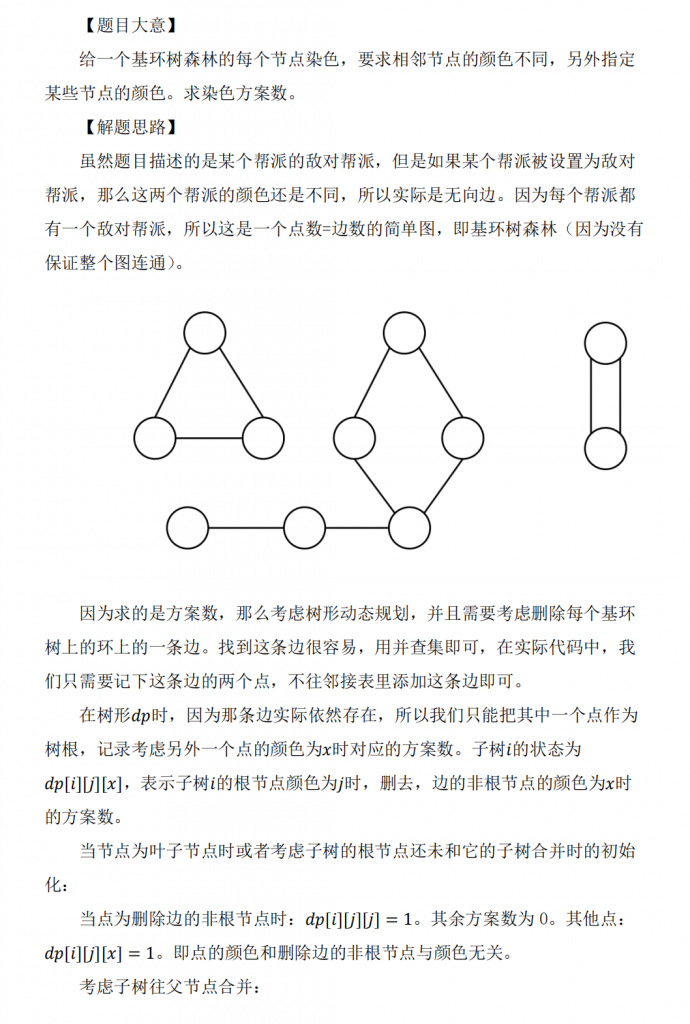
#include <iostream>
#include <cstring>
#include <vector>
using namespace std;
const int mod = 1e9 + 7;
const int N = 200000 + 1;
const int K = 20 + 1;
long long dp[N][K][K]; //i子树、起始节点颜色为j，i节点颜色为k的方案数
long long temp[K][K]; //临时数组
int group[N]; //并查集连通编号
int n, m, k;

int find(int x) { //并查集
	if (x != group[x]) {
		group[x] = find(group[x]);
	}
	return group[x];
}

int sp;  //删除边的非根节点
int color[N]; //强制颜色
vector<int> map[N]; //邻接表
vector<pair<int, int>> pl; //记录所有点对
void dfs(int node, int fa) {
	if (node == sp) { //如果是删除边的非根点需要特别处理
		for (int i = 1; i <= k; i++) {
			dp[node][i][i] = 1;
		}
	} else { //其余点和那个点无关
		for (int i = 1; i <= k; i++)
			for (int j = 1; j <= k; j++) {
				dp[node][i][j] = 1;
			}
	}
	for (int next : map[node])
		if (next != fa) { //转移，考虑子树往父节点合并
			dfs(next, node);
			memset(temp, 0, sizeof temp);
			for (int i = 1; i <= k; i++) {
				for (int j = 1; j <= k; j++) {
					temp[i][j] += dp[node][i][j] * (dp[next][i][0] - dp[next][i][j]) % mod;
				}
			}
			for (int i = 1; i <= k; i++) {
				for (int j = 1; j <= k; j++) {
					dp[node][i][j] = temp[i][j] % mod;
				}
			}
		}
	for (int i = 1; i <= k; i++) { //计算方案和
		for (int j = 1; j <= k; j++) {
			if (color[node] == j || color[node] == 0) { //处理强制规定颜色的点
				dp[node][i][0] += dp[node][i][j];
			} else {
				dp[node][i][j] = 0;
			}
		}
		dp[node][i][0] %= mod;
	}
}

int main() {
	freopen("flag.in", "r", stdin);
	freopen("flag.out", "w", stdout);
	long long ans = 1;
	cin >> n >> m >> k;
	for (int i = 1; i <= n; i++ )
		group[i] = i; //并查集初始化
	for (int i = 1; i <= n; i++) {
		int u,  x, y;
		cin >> u ;
		x = find(i), y = find(u);
		if (x != y) { //如果不连通 ，正常处理
			group[x] = y;
			map[u].push_back(i);
			map[i].push_back(u);
		} else { //如果连通，那么就是我们要找的边
			pl.push_back({ u, i }); //不加入邻接表，记录下点对
		}
	}
	for (int i = 1; i <= m; i++) {
		int p, c;
		cin >> p >> c;
		color[p] = c;
	}
	for (auto p : pl) { //处理每个基环树
		sp = p.first;
		dfs(p.second, 0); //以其中一个点为根进行树形dp
		long long total = 0;
		for (int i = 1; i <= k; i++) { //统计此树内的方案数
			for (int j = 1; j <= k; j++)
				if (i != j) { //需要保证删除的边的两点颜色不同
					total += dp[p.second][i][j];
				}
		}
		ans = ans * (total % mod) % mod; //总方案数为各个树的方案数之积
	}
	if (ans < 0)
		ans += mod;
	cout << ans;
	return 0;
}

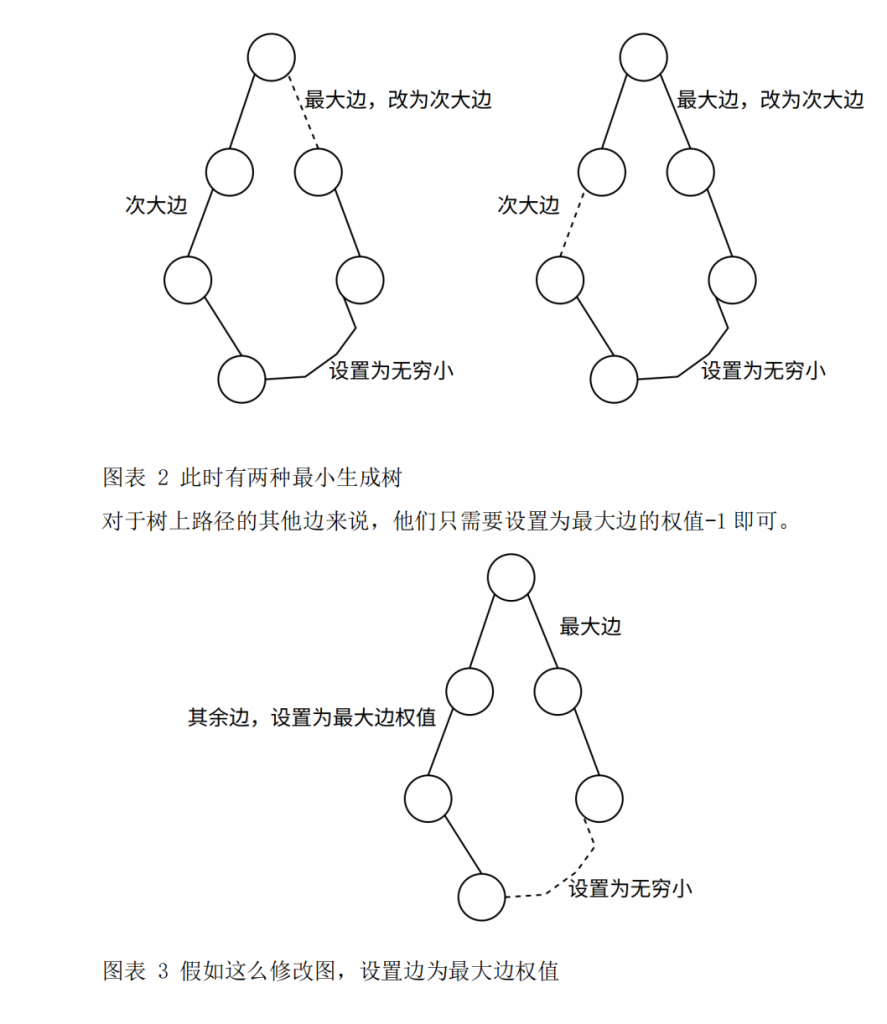
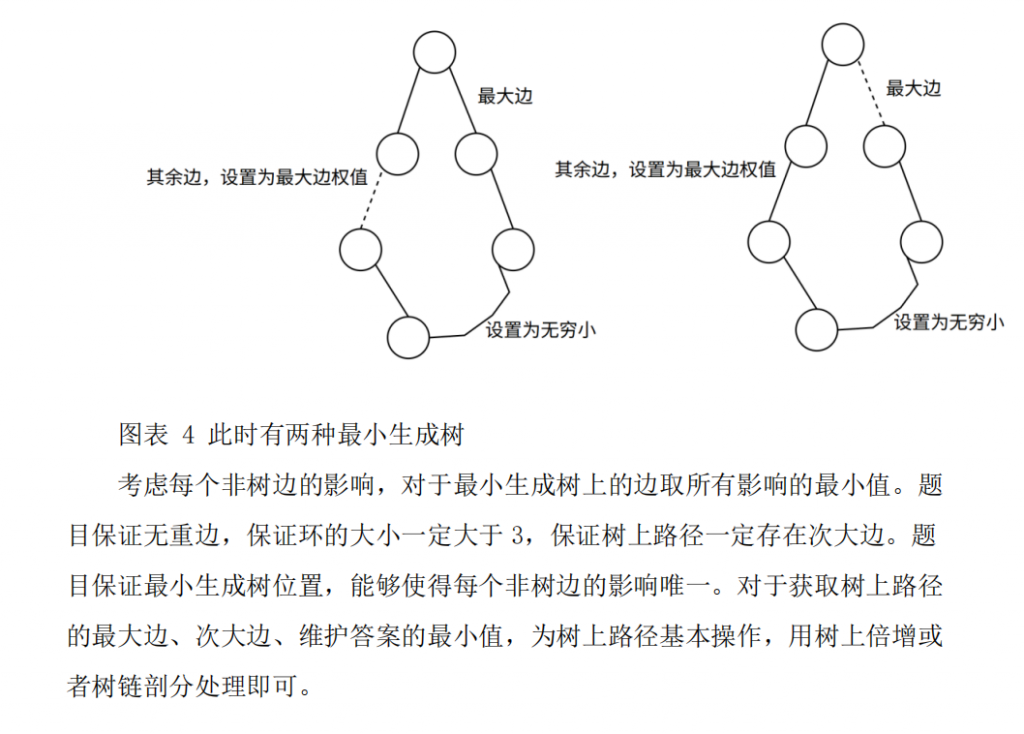
#include <iostream>
#include <algorithm>
#include <vector>
#include <cstring>
#include <fstream>
using namespace std;
const int nsize = 200001;
int n, m;

struct edge {
	int u, v;
	int val;
	int index;
	bool operator <(edge e2) {
		return val < e2.val;
	}
} list[nsize];
bool intree[nsize]; //是否树边
int group[nsize];  //点的连通编号
int ans[nsize];

vector<int>map[nsize]; //最小生成树的邻接表
int find(int x) {
	if (x != group[x]) {
		group[x] = find(group[x]);
	}
	return group[x];
}
//树链剖分模板
int siz[nsize];
int fat[nsize];
int son[nsize];
int dis[nsize], edi[nsize];
int dep[nsize];
int dfn[nsize], rnk[nsize], order;
int top[nsize];

void dfs(int node, int fa) {
	siz[node] = 1;
	dep[node] = dep[fa] + 1;
	fat[node] = fa;
	for (int i : map[node])  {
		int next = (list[i].u == node ? list[i].v : list[i].u);
		if (next != fa) {
			dis[next] = list[i].val;
			dfs(next, node);
			siz[node] += siz[next];
			if (siz[son[node]] < siz[next])
				son[node] = next;
		}
	}
}

void dfs2(int node, int t) {
	top[node] = t;
	dfn[node] = ++order;
	rnk[order] = node;
	if (son[node])
		dfs2(son[node], t);
	for (int i : map[node]) {
		int next = (list[i].u == node ? list[i].v : list[i].u);
		if (next != fat[node] && next != son[node]) {
			dfs2(next, next);
		}
	}
}

int val[nsize * 4][2]; //线段树维护树上路径的最大值和次大值
int lazy[nsize * 4]; //懒标记
void combine(int *res, int *a, int *b) { //合并取最大值和次大值
	int l1 = 0, l2 = 0;
	for (int r1 = 0; r1 < 2; r1++) { //简单的归并排序
		if (dis[rnk[a[l1]]] > dis[rnk[b[l2]]]) {
			res[r1] = a[l1];
			l1++;
		} else {
			res[r1] = b[l2];
			l2++;
		}
	}
}

//线段树建树
void makeTree(int node, int left, int right) {
	if (left == right) {
		val[node][0] = left;
	} else {
		int mid = (left + right) / 2;
		makeTree(node * 2, left, mid);
		makeTree(node * 2 + 1, mid + 1, right);
		combine(val[node], val[node * 2], val[node * 2 + 1]);
	}
}

//查询树链
void query(int node, int left, int right, int qleft, int qright, int *res) {
	if (qleft <= left && right <= qright) {
		res[0] = val[node][0];
		res[1] = val[node][1];
	} else if (left > qright || qleft > right)
		return;
	else {
		int mid = (left + right) / 2;
		int res1[2] = {0, 0}, res2[2] = { 0, 0 };
		query(node * 2, left, mid, qleft, qright, res1);
		query(node * 2 + 1, mid + 1, right, qleft, qright, res2);
		combine(res, res1, res2);
	}
}

//懒标记下放
void pushdown(int node) {
	lazy[node * 2] = min(lazy[node * 2], lazy[node]);
	lazy[node * 2 + 1] = min(lazy[node * 2 + 1], lazy[node]);
}

//设置影响值，区间
void edit(int node, int left, int right, int eleft, int eright, int val) {
	if (lazy[node] < val)
		return;
	else if (eleft <= left && right <= eright) {
		lazy[node] = val;
	} else {
		int mid = (left + right) / 2;
		pushdown(node);
		if (eleft <= mid)
			edit(node * 2, left, mid, eleft, eright, val);
		if (eright > mid)
			edit(node * 2 + 1, mid + 1, right, eleft, eright, val);
		lazy[node] = max(lazy[node * 2], lazy[node * 2 + 1]);
	}
}

//单点设置影响值
void edit2(int node, int left, int right, int index, int val) {
	if (left == right) {
		lazy[node] = min(lazy[node], val);
	} else {
		int mid = (left + right) / 2;
		pushdown(node);
		if (index <= mid)
			edit2(node * 2, left, mid, index, val);
		if (index > mid)
			edit2(node * 2 + 1, mid + 1, right, index, val);
		lazy[node] = max(lazy[node * 2], lazy[node * 2 + 1]);
	}
}

//获得所有树上边的允许最大值
void allpush(int node, int left, int right) {
	if (left == right) {
		if (lazy[node] != 0x3f3f3f3f)
			edi[left] = lazy[node];
		else
			edi[left] = -1; //如果依然是默认最大值，那么就是最小生成树
	} else {
		int mid = (left + right) / 2;
		pushdown(node);
		allpush(node * 2, left, mid);
		allpush(node * 2 + 1, mid + 1, right);
	}
}

//获取树上路径的最大和次大值，返回到res数组中
void getMaxEdge(int x, int y, int *res) {
	int temp[2] ;
	while (top[x] != top[y]) {
		if (dep[top[x]] > dep[top[y]]) {
			int res1[2] = { 0, 0 };
			query(1, 1, n, dfn[top[x]], dfn[x], res1);
			combine(temp, res, res1);
			res[0] = temp[0], res[1] = temp[1];
			x = fat[top[x]];
		} else {
			int res1[2] = { 0, 0 };
			query(1, 1, n, dfn[top[y]], dfn[y], res1);
			combine(temp, res, res1);
			res[0] = temp[0], res[1] = temp[1];
			y = fat[top[y]];
		}
	}
	if (dep[x] > dep[y]) {
		int res1[2] = { 0, 0 };
		query(1, 1, n, dfn[y] + 1, dfn[x], res1);
		combine(temp, res, res1);
		res[0] = temp[0], res[1] = temp[1];
	} else {
		int res1[2] = { 0, 0 };
		query(1, 1, n, dfn[x] + 1, dfn[y], res1);
		combine(temp, res, res1);
		res[0] = temp[0], res[1] = temp[1];
	}
}

//设置树上路径的允许值
void setEdge(int x, int y, int val) {
	while (top[x] != top[y]) {
		if (dep[top[x]] > dep[top[y]]) {
			edit(1, 1, n, dfn[top[x]], dfn[x], val);
			x = fat[top[x]];
		} else {
			edit(1, 1, n, dfn[top[y]], dfn[y], val);
			y = fat[top[y]];
		}
	}
	if (dep[x] > dep[y]) {
		edit(1, 1, n, dfn[y] + 1, dfn[x], val);
	} else {
		edit(1, 1, n, dfn[x] + 1, dfn[y], val);
	}
}

int main() {
	cin >> n >> m;
	for (int i = 1; i <= n; i++)
		group[i] = i; //并查集
	for (int i = 1; i <= m; i++) {
		cin >> list[i].u >> list[i].v >> list[i].val;
		list[i].index = i;
	}
	memset(lazy, 0x3f, sizeof lazy);
	sort(list + 1, list + m + 1);
	int cnt = 0;
	for (int i = 1; cnt < n - 1; i++) { //kruskal求最小生成树
		int x = find(list[i].u);
		int y = find(list[i].v);
		if (x != y) {
			map[list[i].u].push_back(i);
			map[list[i].v].push_back(i);
			intree[i] = true; //记录树边
			group[x] = group[y];
			cnt++;
		}
	}
	dfs(1, 0);
	dfs2(1, 1);
	makeTree(1, 1, n);
	for (int i = 1; i <= m; i++) {
		if (!intree[i]) { //枚举所有非树边
			int res[2] = {0, 0};
			getMaxEdge(list[i].u, list[i].v, res); //查询最大边编号和次大边
			ans[list[i].index] = dis[rnk[res[1]]] - 1; //此非树边的权值为次大边-1
			setEdge(list[i].u, list[i].v, dis[rnk[res[0]]] - 1); //先所有树边设置权值为最大边-1
			edit2(1, 1, n, res[0], dis[rnk[res[1]]] - 1); //最大边设置为次大边-1
		}
	}
	allpush(1, 1, n);
	for (int i = 1; i <= m; i++) {
		if (intree[i]) {
			if (fat[list[i].u] == list[i].v) {
				ans[list[i].index] = edi[dfn[list[i].u]];
			} else {
				ans[list[i].index] = edi[dfn[list[i].v]];
			}
		}
	}
	for (int i = 1; i <= m; i++)
		cout << ans[i] << " ";
	return 0;
}