2024年云南省青少年编程精英赛提高组题解

T1.异或（xor）

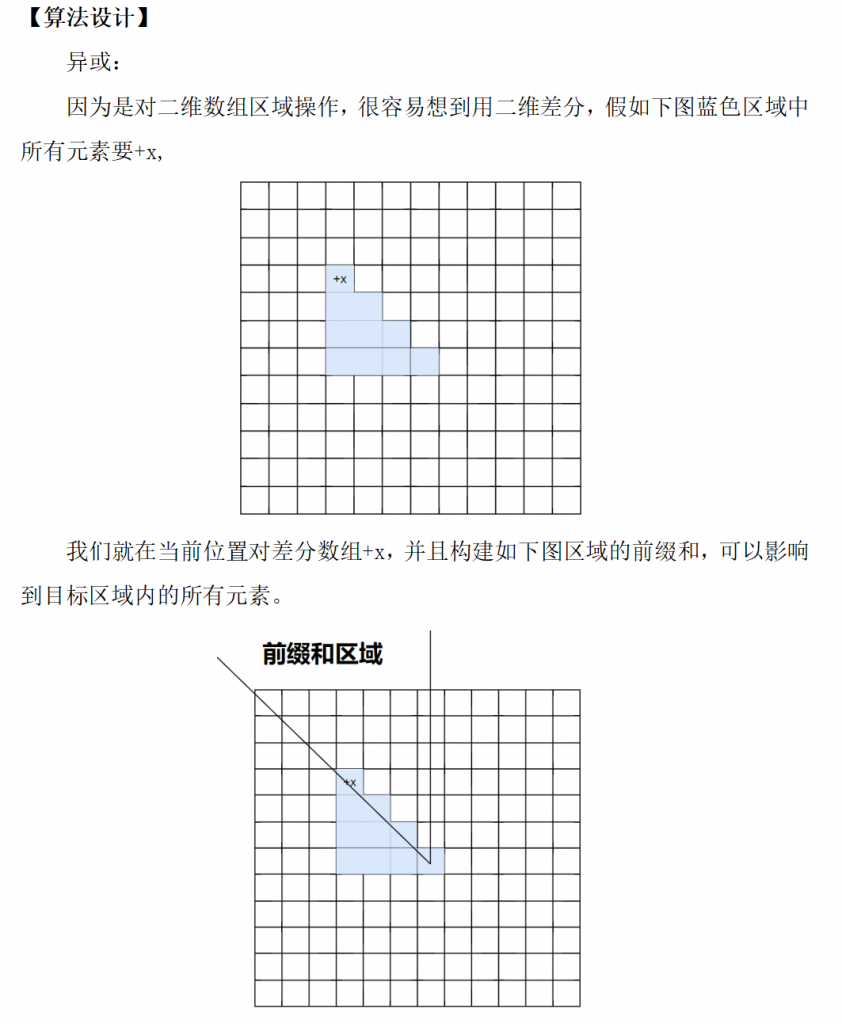
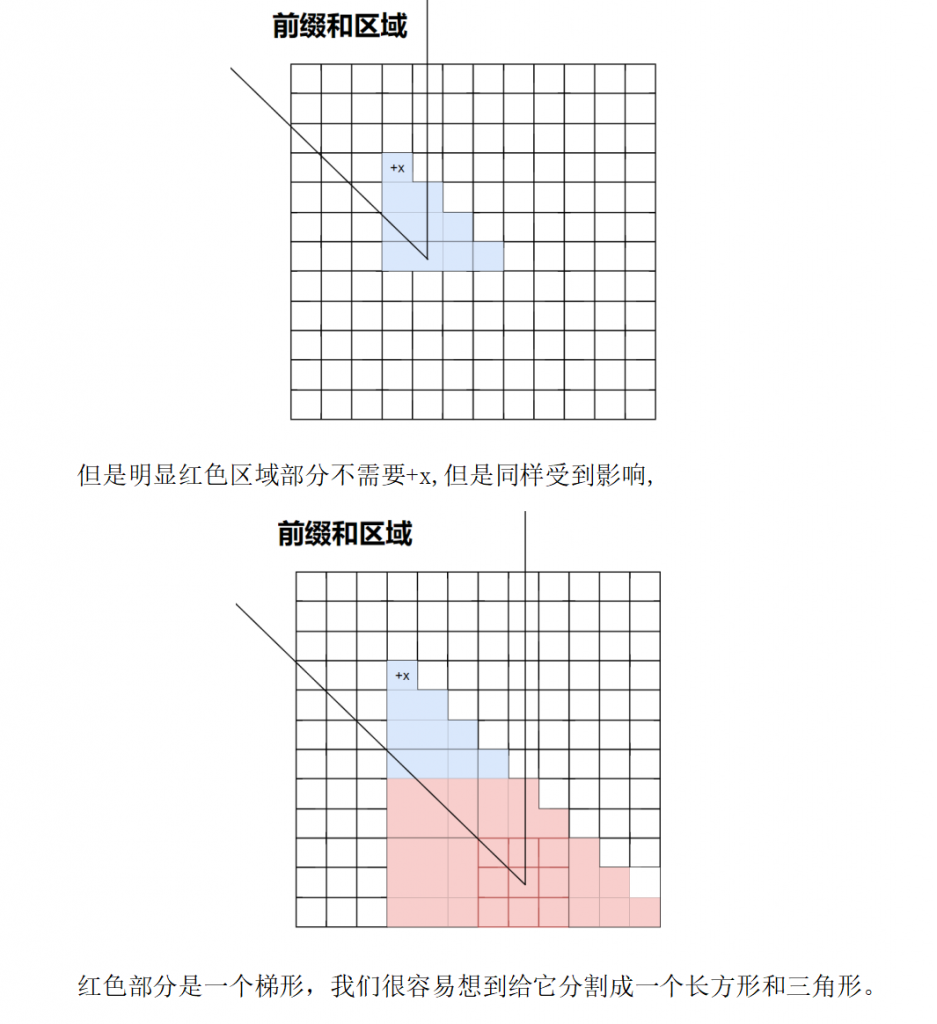
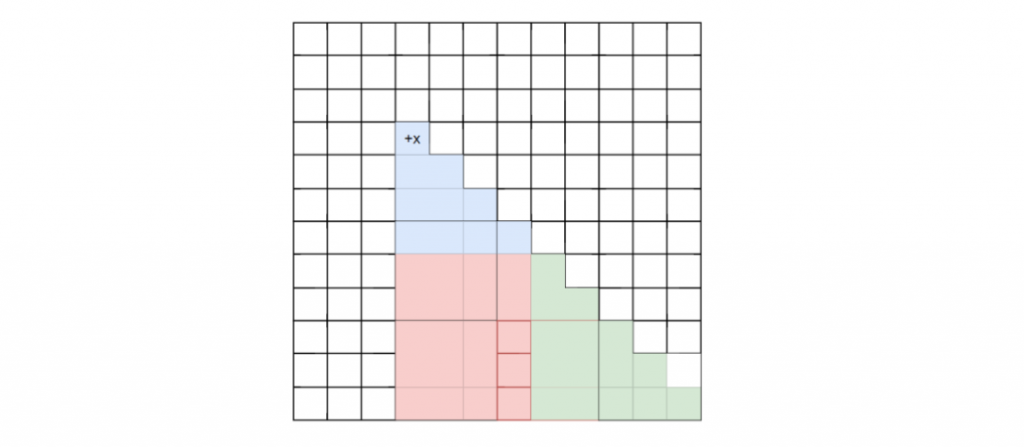
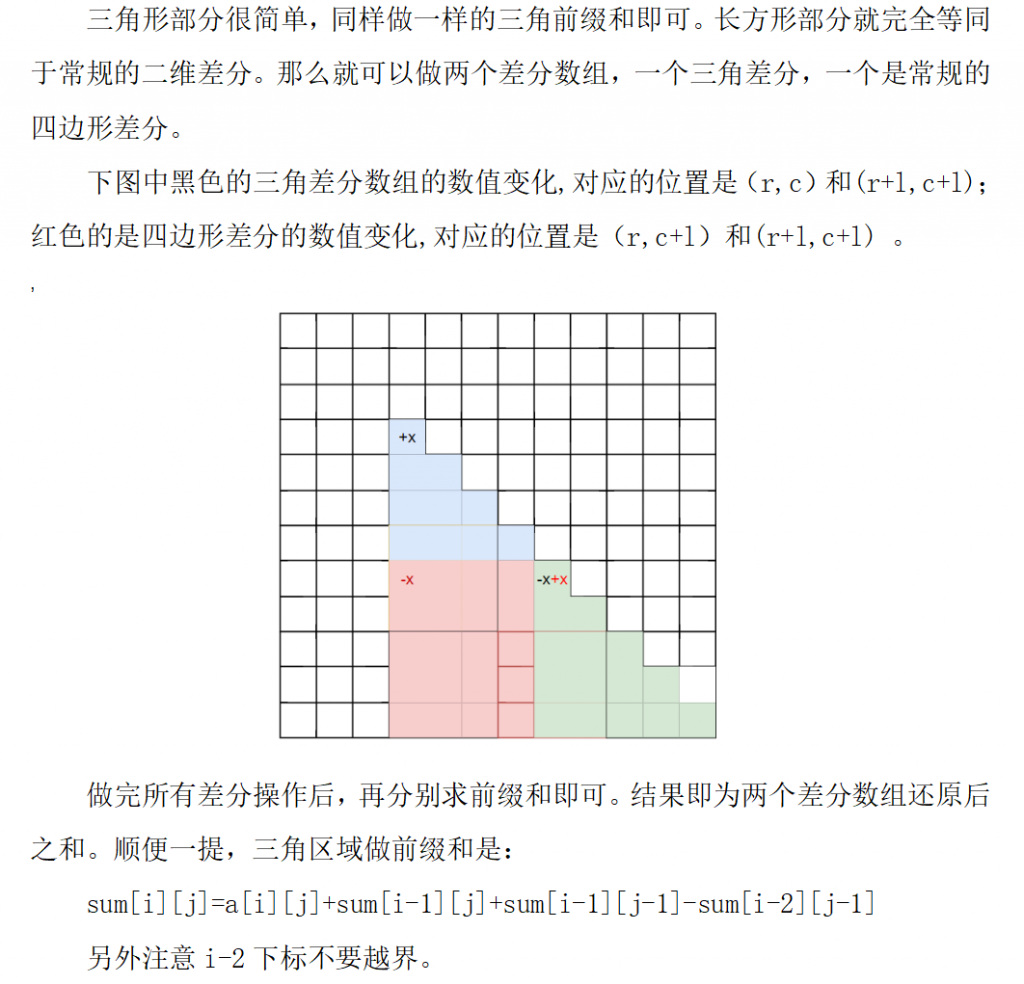
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e3 + 10;
int n, q;
ll a[maxn][maxn], b[maxn][maxn], ans;

inline void add_a(int x, int y, int v) {
  if (x <= n && y <= n)
    a[x][y] += v;
}

inline void add_b(int x, int y, int v) {
  if (x <= n && y <= n)
    b[x][y] += v;
}

int main() {
  freopen("xor.in", "r", stdin);
  freopen("xor.out", "w", stdout);
  scanf("%d%d", &n, &q);
  while (q--) {
    int r, c, l, s;
    scanf("%d%d%d%d", &r, &c, &l, &s);
    add_a(r, c, s);
    add_a(r + l, c + l, -s);
    add_b(r + l, c, -s);
    add_b(r + l, c + l, s);
  }
  for (int i = 1; i <= n; ++i)
    for (int j = 1; j <= n; ++j) {
      if (i > 1)
        a[i][j] += a[i - 1][j - 1] + a[i - 1][j] - a[i - 2][j - 1];
      else
        a[i][j] += a[i - 1][j - 1] + a[i - 1][j];
      b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];
      ans ^= a[i][j] + b[i][j];
    }
  printf("%lld\n", ans);
  return 0;
}

T2.前缀和(sum)

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e5+5;
int a[N],n,x,tree[N];
struct node{
	int sum,r;//sum记录前缀和，r记录sum是前r个数的前缀和
}p[N];
int lobit(int x){
	return x & -x;
}
void update(int x)
{
	for(int i=x;i<=n;i+=lobit(i)){
		tree[i]++;
	}
}
int query(int x)
{
	int sum = 0;
	for(int i=x;i>=1;i-=lobit(i)){
		sum+=tree[i];
	}
	return sum;
}
bool cmp(node a,node b){
	return a.sum<b.sum;
}
signed main()
{
	cin>>n>>x;n++;
	for(int i=2;i<=n;i++){
		cin>>a[i];
		p[i].sum = p[i-1].sum+a[i];
		p[i].r = i;
	} 
	p[1].r = 1;p[1].sum = 0;
	sort(p+1,p+n+1,cmp);//从小到大排序
	int l = 1,res = 0;
    //双指针
	for(int i=1;i<=n;i++){
		while(l<=n && p[i].sum-p[l].sum>=x)update(p[l].r),l++;
		if(p[i].r)res+=query(p[i].r);
	}
	cout<<res<<endl;
	return 0;
 } 

T3.连通块（connect）

#include <bits/stdc++.h>
using namespace std;
int p1 = 2000000;
char buf[2000005];

int gc() {
  if (p1 >= 2000000)
    fread(buf, 1, 2000000, stdin), p1 = 0;
  return buf[p1++];
}

int rd() {
  int x = 0;
  char ch = gc();
  while (ch < '0' || ch > '9')
    ch = gc();
  while (ch <= '9' && ch >= '0')
    x = x * 10 + ch - '0', ch = gc();
  return x;
}
int n, a[100005], mnp[10000005], h[2100005], cnt, ans, fa[2100005], sz[2100005], id[10100005], M;
int dfn[2100005], low[2100005], st[2100005], top, sign, sz2[2100005], ALL;
bitset<10100005> vst;

struct E {
  int to, nxt;
} e[7200005];

void Add(int x, int y) {
  e[++cnt] = {y, h[x]}, h[x] = cnt;   //链式前向星存储图
}

int gf(int x) {
  while (fa[x] && fa[fa[x]])
    x = fa[x] = fa[fa[x]];    //并查集
  if (fa[x])
    x = fa[x];
  return x;
}

void Merge(int x, int y) { //并查集合并
  x = gf(x), y = gf(y);
  if (x ^ y)
    fa[x] = y, sz[y] += sz[x];
}

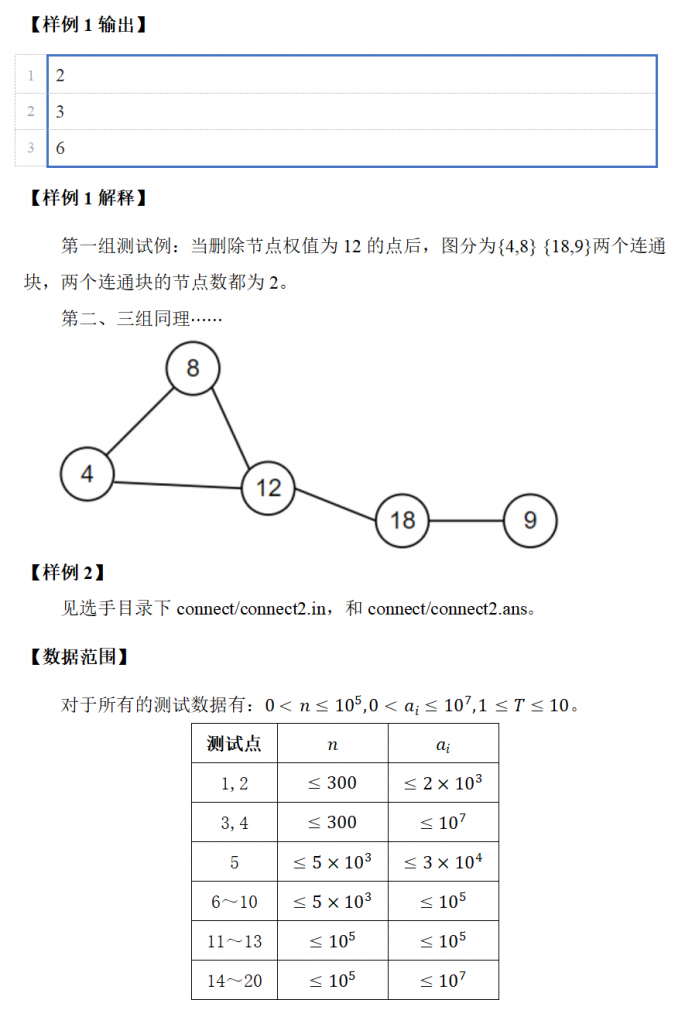
void Tarjan(int x, int fa) { //tarjan求割点
  dfn[x] = low[x] = ++sign, st[++top] = x, sz2[x] = 0;
  int mx = 0, cc = 0;
  for (int i = h[x]; i; i = e[i].nxt) {
    if (i == (fa ^ 1))
      continue;
    int y = e[i].to;
    if (!dfn[y]) {
      Tarjan(y, i), low[x] = min(low[x], low[y]);
      if (low[y] > dfn[x])
        assert(st[top] == y), top--, mx = max(mx, sz2[y]), sz2[x] += sz2[y],
                                     cc++; //如果low序>=dfn序则为割点，需要计算分割后的节点数
      else if (low[y] == dfn[x]) {
        int t, sum = 0;
        do
          t = st[top--], sz2[x] += sz2[t], sum += sz2[t];
        while (t != y);
        cc++, mx = max(mx, sum);
      }
    } else
      low[x] = min(low[x], dfn[y]);
  }
  if (x <= n) { //如果是另外加的简单合数点，则不需要考虑
    sz2[x]++;
    if ((fa && cc) || (!fa && cc > 1))
      ans = min(ans, max(mx, ALL - sz2[x]));
    else
      ans = min(ans, ALL - 1); //如果不是割点，则视为只是单单取了这个点
  }
}

void Solve() {
  cnt = 1, sign = top = 0, memset(h, 0, sizeof(h)), memset(fa, 0, sizeof(fa)), memset(sz, 0, sizeof(sz)), memset(dfn, 0,
                        sizeof(dfn));
  n = rd();
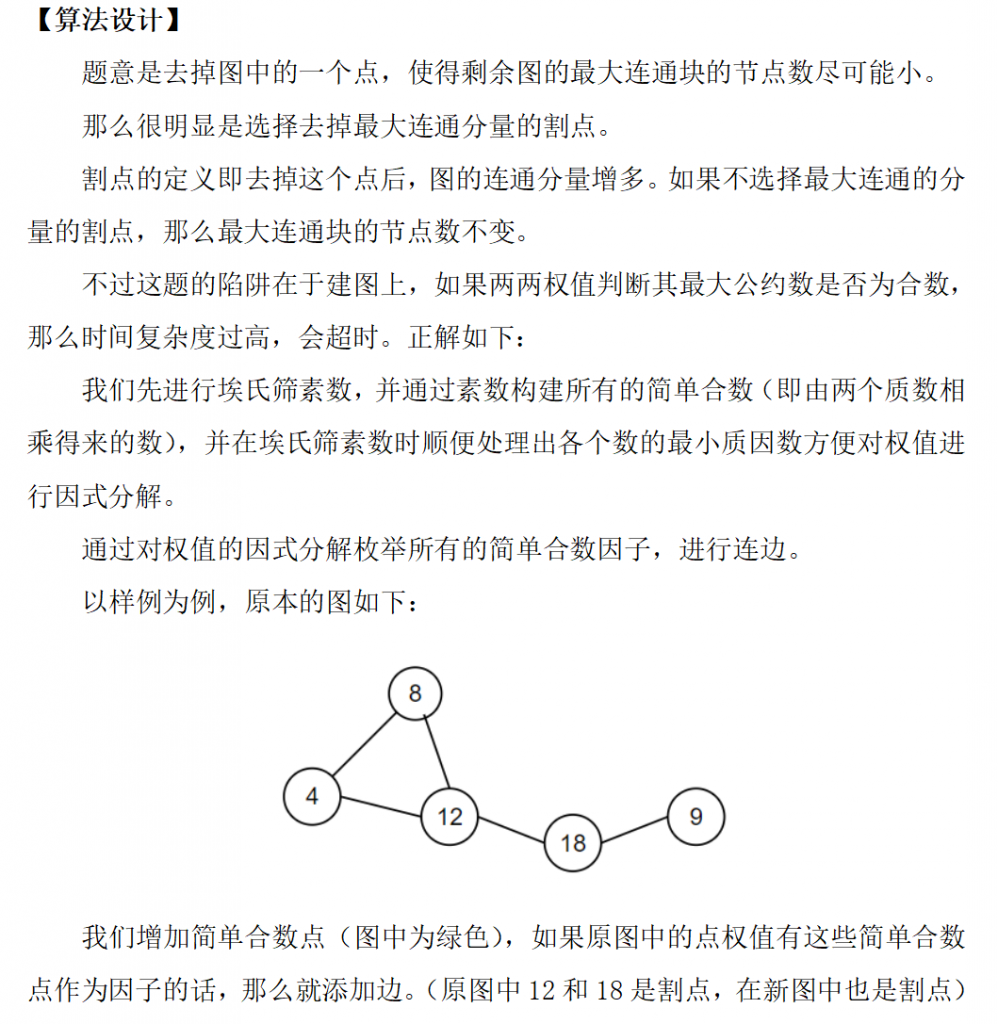
  for (int i = 1; i <= n; i++) {
    int p[10] = {0}, C[10] = {0}, x;
    x = rd(), sz[i] = 1;
    while (x > 1) { //因式分解
      int u = mnp[x];
      p[++p[0]] = u;
      while (x % u == 0)
        x /= u, C[p[0]]++; //统计质因子的幂次
    }
    for (int j = 1; j <= p[0]; j++) //两两枚举质因子，那么这个数就有这个简单合数的作为因子
      for (int k = j + (C[j] <= 1); k <= p[0]; k++) //注意因子的幂次为1的情况
        if (1ll * p[j]*p[k] <= 10000000)
          Add(i, id[p[j]*p[k]] + n), Add(id[p[j]*p[k]] + n, i), Merge(i, id[p[j]*p[k]] + n); //添加边，和并查集合并
  }
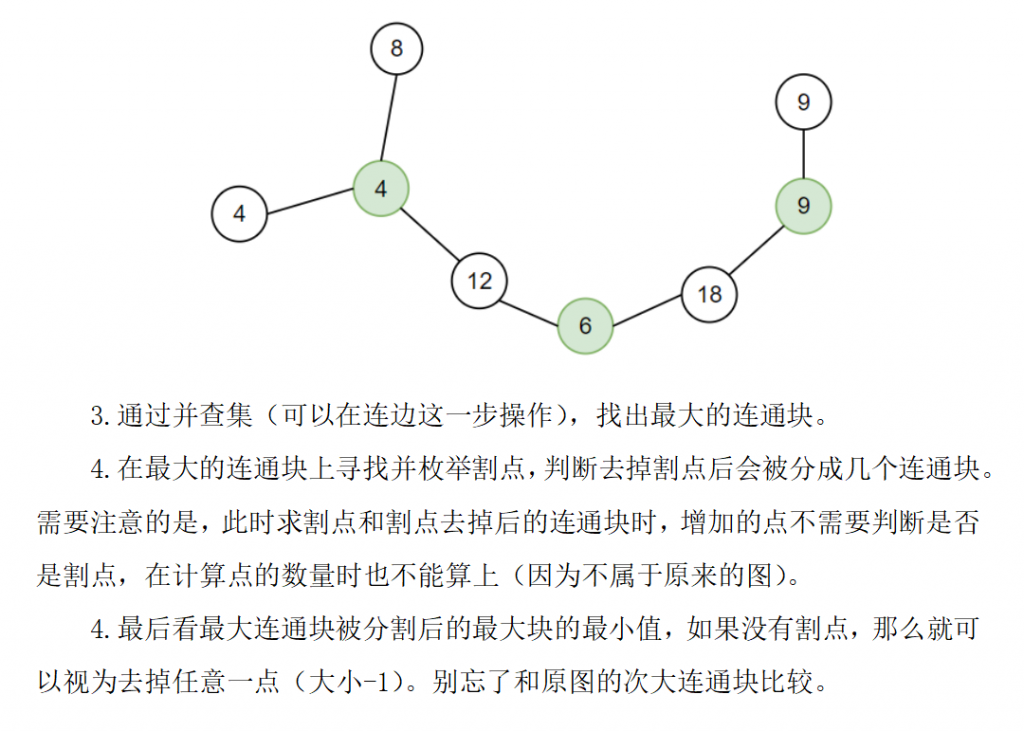
  int mx = 0, se = 0, mxp = 0; //统计最大连通块和次小连通块的节点数
  for (int i = 1; i <= M + n; i++) {
    if (fa[i] || !sz[i])
      continue;
    if (sz[i] > mx)
      se = mx, mx = sz[i], mxp = i;
    else if (sz[i] > se)
      se = sz[i];
  }
  ans = mx, ALL = mx, Tarjan(mxp, 0), cout << max(ans, se) << '\n'; //求割点
}

int main() {
  freopen("connect.in", "r", stdin);
  freopen("connect.out", "w", stdout);
  for (int i = 2; i <= 10000000; i++) { //埃氏筛素数
    if (vst[i])
      continue;
    mnp[i] = i;
    if (1ll * i * i > 10000000)
      continue;
    int I = i * (1 + (i != 2));
    for (int j = i * i; j <= 10000000; j += I)
      vst[j] = 1, mnp[j] = (!mnp[j] ? i : mnp[j]); //记录最小质因子
  }
  for (int i = 2; i <= 10000000; i++)
    if (vst[i] && !vst[i / mnp[i]]) //如果一个数不是质数但是除以其最小质因子后是质数则是简单合数
      id[i] = ++M; //给其编号
  int t = rd();
  while (t--)
    Solve();
}

T4.Nim博弈（nim）

#include<iostream>  
#include<fstream>
using namespace std; 
const int len = 11; //数值不超过2024，那么最多二进制11位
int d[200001];  
int maxnode=0;
struct TreeNode {
  int left;
  int right;
  int total[len]; //维护区间内二进制的第i位是1的个数
  int lazy; //懒标记，维护叶节点待异或的值
  TreeNode operator + (TreeNode n2) {
    TreeNode t;
    for (int i = 0; i < len; i++) t.total[i] = total[i] + n2.total[i];
    return t;
  }
}tlist[800010];
void pushdown(int node) { //懒标记更新
  if (tlist[node].lazy) {
    for (int i = 0; i < len; i++) if (tlist[node].lazy>>i & 1){
      //如果需要异或的值的某一位是1，那么对于区间内的所有数字那一位是1的都变成0，是0的都变成1，那么1的个数即=区间长度-原有数字个数。（0是保持，则不用处理）
      tlist[node * 2].total[i] = tlist[node * 2].right - tlist[node * 2].left + 1 - tlist[node * 2].total[i]; 
      tlist[node * 2 + 1].total[i] = tlist[node * 2 + 1].right - tlist[node * 2 + 1].left + 1 - tlist[node * 2 + 1].total[i];
    } 
    tlist[node * 2].lazy ^= tlist[node].lazy; //别忘了子节点的懒标记也更新
    tlist[node * 2 + 1].lazy ^= tlist[node].lazy;
    tlist[node].lazy = 0;
  }
}
void update(int node) {
  for (int i = 0; i < len; i++) tlist[node].total[i] = tlist[node * 2].total[i] + tlist[node * 2 + 1].total[i]; //子节点汇总
}
void makeTree(int node,int left, int right) {
  if (left == right) {
    tlist[node].left = left;
    tlist[node].right = right;
    tlist[node].lazy = 0;
    for (int j = 0; j < len; j++) tlist[node].total[j] = (d[left] >> j) & 1; //建树即按位拆分
  }
  else {  
    tlist[node].left = left;
    tlist[node].right = right;
    tlist[node].lazy = 0;
    int mid = (left + right) / 2;
    makeTree(node * 2, left, mid);
    makeTree(node * 2 + 1, mid + 1, right);
    update(node);
  }
}
void xorArea(int node, int left, int right ,int value,int xleft,int xright) {
  if (xleft <= left && right <= xright) {
    //如果需要异或的值的某一位是1，那么对于区间内的所有数字那一位是1的都变成0，是0的都变成1，那么1的个数即=区间长度-原有数字个数。（0是保持，则不用处理）
    for (int i = 0; i < len; i++) if (value >> i & 1)
      tlist[node].total[i] = tlist[node].right - tlist[node].left + 1 - tlist[node].total[i];
    tlist[node].lazy ^= value;
  }
  else if (left > xright || right < xleft) return;
  else {
    int mid = (left + right) / 2;
    pushdown(node);
    xorArea(node * 2, left, mid, value, xleft, xright);
    xorArea(node * 2 + 1, mid + 1, right, value, xleft, xright);
    update(node);
  }
}
void change(int node, int left, int right, int p, int value) {
  if (left == right) { 
    for (int j = 0; j < len; j++) tlist[node].total[j] = (value >> j) & 1; //按位拆分
  }
  else {
    int mid = (left + right) / 2;
    pushdown(node);
    if (p<=mid) change(node * 2, left, mid, p, value );
    else change(node * 2 + 1, mid + 1, right, p, value);
    update(node);
  }
}
TreeNode query(int node, int left, int right, int qleft, int qright) {
  if (qleft <= left && right <= qright) {  
    return tlist[node];
  }
  else if (left > qright || right < qleft ) return tlist[0];
  else {
    int mid = (left + right) / 2;
    pushdown(node);
    return query(node * 2, left, mid, qleft, qright ) + query(node * 2 + 1, mid + 1, right, qleft, qright);
  }
}
int main() {   
  freopen("nim.in", "r", stdin);
  freopen("nim.out", "w", stdout);
  int n, m, left, right, value;
  cin >> n >> m;
  string op;
  for (int i = 1; i <= n; i++) cin >> d[i];
  makeTree(1, 1, n);
  for (int i = 0; i < m; i++) {
    cin >> op;
    if (op == "xor") {
      cin >> left >> right >> value;
      xorArea(1, 1, n, value, left, right);
    }
    else if (op == "set") {
      cin >> left >> value;
      change(1, 1, n, left, value);
    }
    else if (op == "game") {
      cin >> left >> right;
      TreeNode ans = query(1, 1, n, left, right);
      for (int i = len - 1; i >= 0; i--) {
        if (ans.total[i] % 2) { //高位往低位处理，直到第一位的个数是奇数的
          cout << "true " << ans.total[i] << endl;
          break;
        }
        if (i == 0) { //如果所有位是1的数字个数都是偶数
          cout << "false" << endl;
        }
      }
    }
  }
  return 0;
}